4枚カード問題(ウェイソン選択課題)

4枚カード問題とは、人間の推論を調べる課題です。認知心理学の実験で良く用いられます。理系大学生でも正答率が高くないという結果が多く報告されています。問題は以下のようなものです。

4枚のカードがあり、それぞれ片面にはアルファベットが、もう片面には数字が書かれている。

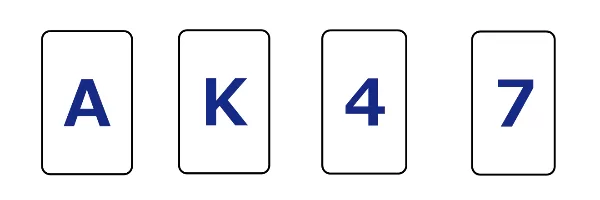
A,K,4,7が見えている状態である。(ここまでは確認済みとする。)
このとき、「片面が母音ならば、そのカードのもう一方の面は偶数でなければならない」というルールが成立しているかどうかを調べたい。

答えの前に注意：この問題の主題は論理学での正解が何かではありません。解答の偏りについて考察することが主題です。

論理学での正解は、「A」と「7」。ルールは、母音と奇数が同じカードを禁止しているので、「Aの裏が偶数か？」と、「7の裏が母音か？」を調べるのが正解。(問題には最小限の枚数とは書いていないので、Aと7を含めていれば正解としてよいと思います。)

よくある解答

4枚カード問題(ウェイソン選択課題)に対しては、「A」と「4」とする解答がよく見受けられます。「4」のカードは常に条件を満たします。このカードを調べても、条件を満たすことを確認するだけです。心理学では確証バイアスと呼ばれています。人間の思考パターンには、正しいケースを確認して満足する、という傾向があるようです。

解答が偏る点が認知心理学的には重要

論理学での正解である「A」と「7」を選ぶ人ももちろんいますが、論理学では誤答となる解答「A」と「4」が頻出します。解答に偏りが出る、ということには何らかの理由がある、と考えられます。

「（正解が何かではなく）なぜ論理的には誤答な解答を選ぶ傾向があるか」を考え、そこから人間の思考パターンについて理解を深めようとするのが心理学です。ミュラーリヤーの錯視では、「長さは実は等しい」ことよりも、「なぜ片方を長いと認識するのか」を考えますね。それと同じように考えてください。

確証バイアス

4枚カードに話を戻します。「4」のカードは、もう片方の面が母音でも子音でも「ルールを満たしている」ため、調べる必要はありません。しかし、調べたくなる人が多くいる、ということです。人間の思考パターンには、正しいことを確認して満足する、という傾向があるようです。「ルールを満たしているケースを調べる」傾向を、心理学では確証バイアスと呼んでいます。確証バイアスにより、『ルールを満たしている「4」をチェックする(論理的にはチェック不要)、一方でルール違反の可能性がある「7」のチェックを行わない』という典型的な解答が発生します。

日常的なテーマだと正答率が上昇

4枚カード問題と論理構造が同一な問題を、身近な話題で試してみると、正答率が上昇することが報告されています。例えば下の問題はどうでしょう。

4人が飲物を飲んでいる。

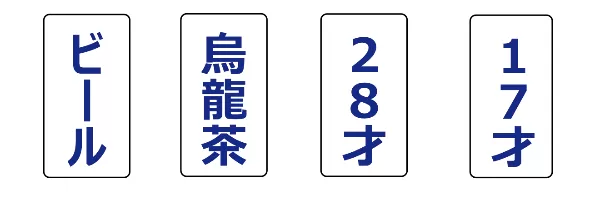
ビールを飲んでいる人	調べる・調べない
烏龍茶を飲んでいる人	調べる・調べない
28才の人	調べる・調べない
17才の人	調べる・調べない

「アルコール飲料を飲んでいるならば、20才以上でなければならない」というルールが成立しているかどうかを確かめたい。

答えは「ビールを飲んでいる人」と「17才の人」です。アルコール飲料の例は、論理学上は4枚カードと同じ問題です。しかし、ルール判定する社会的文脈が想起しやすい、という点で異なります。このようなとき、正答率は大幅に上がる、という実験結果が出ています。人間は、どうやら純粋に論理的な推論を行っているのではないようです。

コスミデス＆トゥービーは、裏切り者検知、という観点で、アルコールと年齢のケースで正答率上がる、という主張をしています。

Johnson-Laird&Wasonのウェイソンの4枚カード問題は、現在も研究が続いている問題です。もっとも、認知科学や心理学における有名な問題の多くがそうですが。また最近では、心理学の影響を受けている行動経済学でも取り上げられることがあるようです。

他にも数学・確率関係では面白いものがありますね。同じ誕生日の人がいる確率などです。

箱ひげ図

箱ヒゲ図作成ツールを公開しています。

ヒストグラムの作成

データを一定の数値幅でグループ化して表示する図の作成ツールです。